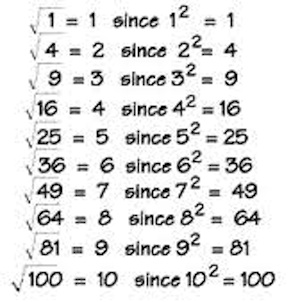This is the root symbol √ . When it includes a number to the right of the symbol like this √4; it is telling us that we must perform the operation of finding the square root of that number.
Finding a Root is the opposite operation of applying exponents. If a number, (for this example we’ll use 4) multiplied by itself, is the square of a number (4² = 16 ); then the square root of 16 is 4. See below for more examples.
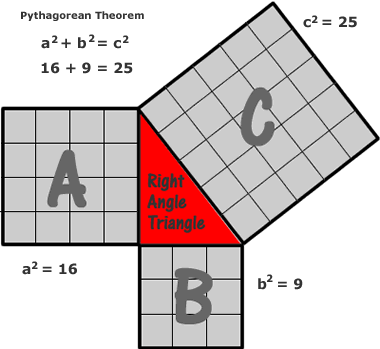
When we use Pythagoras’ Theorem to find the unknown side length of a right triangle; we use the square root operation to determine the side length after finding the total of the two squares on the other two legs of the triangle. See Below:
In the example above, you can see that the side lengths of this right triangle equal the square root of each square.
A = √16 = 4 The side length of A = 4 units
B = √9 = 3 The side length of B = 3 units
C = √25 = 5 The side length of C = 5 units
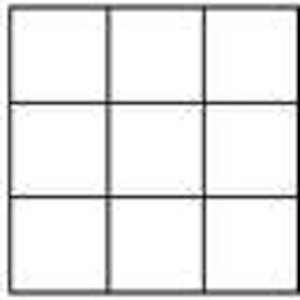
Why do we call certain numbers square numbers? It’s simple – Some numbers can form an array of units that create a square.
So for instance, if you take three square units (for this example units are little 1×1 squares); and you place them side by side in a horizontal direction and then, add two more square units below each one; you will have created a 3×3 square. This square will be made up of nine total units. Hence, the square root of 9 is 3. Nine is a square number because you can form a square with nine units, if you place them side by side in a 3×3 array. See below for image.
Click on the link below for another demonstration of square roots