Exponents are shorthand for repeated multiplication of the same number by itself. Like this……2 x 2 x 2 = 2³
(the exponent is the 3 – it tells us how many times to repeat the multiplication)
A bit confusing?
Read on to understand more about exponents…….
Exponents are written in superscript ( a small number placed at the upper right side of a regular number ) like this 5 2
This means 5 x 5 ( the small 2 is the exponent and the 5 is called the base )
We say five squared when speaking the term.
There are rules you must apply when working with exponents.
Rules of Exponents
Here is a more detailed explanation of exponents; just in case the first one was unclear…….
Exponents are identified in math, by placing a small superscript number next to the base number; like this: 42 . The 4 is identified as the base. The small number 2 is identified as the exponent.
Mathematical operations involving an exponent such 42 indicate that you must perform a repeated multiplication. You must multiply the base number by itself, the number of times as indicated by the exponent. 42 means you must multiply 4×4.
Do not confuse this with multiplying 4×2. This will lead you to an incorrect answer.
When you see a base number with 2 as the exponent, it is often referred to as a square number.
You may hear the words “four squared” or “four to the second power” or “four to the power of two”. This is simply the way we express the operation in english.
Exponents can be any number (large or small) – the reason we use them is to express a larger number by using the shortcut of expressing it as an exponent.
When you see an exponent like this 4³ – it requires you to repeat the multiplication of four………three times : 4×4×4 = 64 (not 4×3=12)
4³ can be spoken as “four cubed” or “four to the third power” or “four to the power of three”.
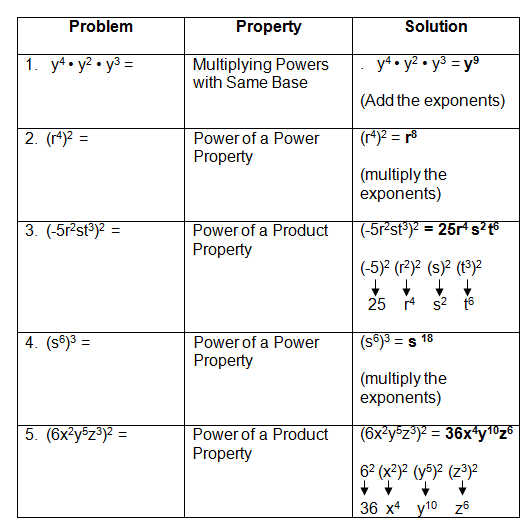
Some mathematical laws of exponents can be found in the matrix below:
Another important rule for evaluating expressions with exponents that contain negative integers with brackets:
- Simplify (–3)2
(–3)2 = (–3)(–3) = (+3)(+3) = 9
Note the difference between the above exercise and the following:
- Simplify –32
–32 = –(3)(3) = -1(3) (3) = (-3) (3) = –9
without brackets, the negative sign only applies to the first integer in the repeated multiplication. Furthermore, when there is a negative sign alone in front of brackets; you can assume that there is a # 1 next to it (as seen in the example)
Therefore a negative integer raised to any power (without brackets) will always be negative.